Sensor and Radiation Shield Comparison Calculator for Temperature Error
/Sensor comparisons focusing only on average, maximum and minimum values can be deceiving when dealing with sensors with differing response times, especially in atmospheric temperature measurement.
While fan-aspirated solar radiation shields seem to minimize this problem, they come at a cost of reliability and accuracy in many rainy, foggy, snowy and wet weather conditions where naturally ventilated shields excel. The one exception currently being the the double helical MeteoShield Professional which in WMO studies like the “Intercomparison of Shelters in the RMI AWS Network” has shown to be more accurate than even fan-aspirated radiation shields and screens. It has the lowest time constant (shortest response time) of any naturally ventilated solar radiation shield to date.
Naturally ventilated solar radiation shields don’t suck in airborne water droplets and dirt onto the internal temperature and humidity sensors, thus extending their accuracy lifetime and long-term stability.
Web calculator for comparing two different sensor response times
Comparison of sensor response times and resulting temperature error calculator computes the effect of different sensor response times on recorded maximum, minimum and average (mean) air temperatures and the resulting measurement errors.
Calculator of the influence of sensor response time (τ 63.2%) on error in climatic temperature measurements computes the measurement error of a sensor and radiation shield combination and individual contributions to the error due to each instrument’s response time.
NOTE: Temperature sensor response time is the time it takes a sensor value to reach 93.3% of a temperature step change. The sensor time constant τ is the time it takes for the sensor value to reach only 63.2% of the same step change in temperature. For a detailed explanation of the difference between the “sensor time constant” and “sensor response time” see the following article “The difference between sensor response time and sensor time constant τ (tau) 63.2%.”
Measuring climatic air temperature example
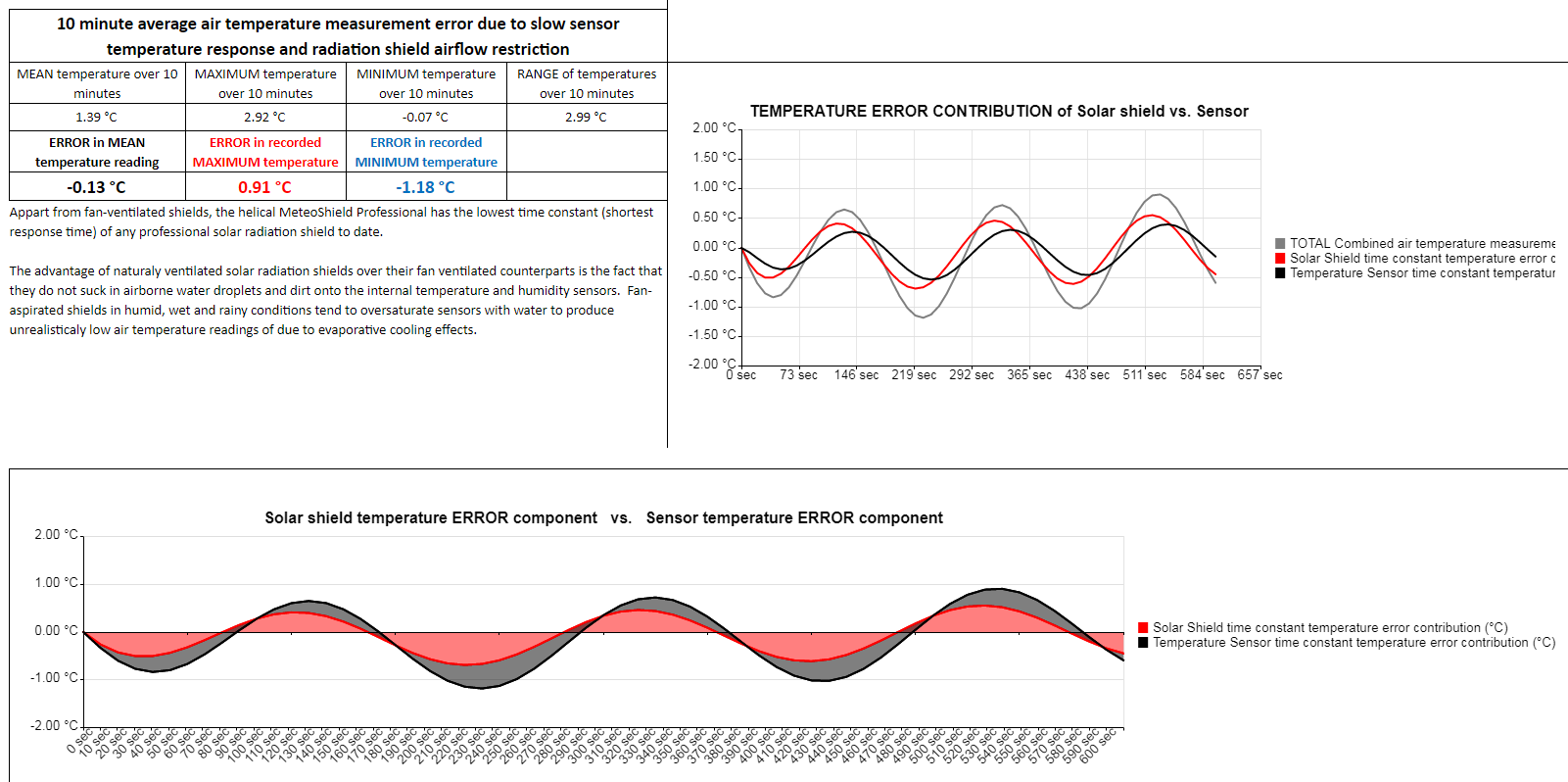
For a temperature rise of a 2°C over a 10 minute period, average (mean) air temperature measurement error increases from -0.07°C to -0.13°C due to a change in time constant τ (tau) from 10 to 30 seconds.
Same positive temperature change increases the measured 10 minute maximum temperature error from -0.04°C to -0.08°C.
For a temperature drop of a -2°C over a 10 minute period, average (mean) air temperature measurement error increases from +0.07°C to +0.13°C due to a change in time constant τ (tau) from 10 to 30 seconds.
Same negative temperature change increases the measured 10 minute minimum temperature from +0.04°C to +0.08°C.
Conclusions
Temperature maximums are underestimated and temperature minimums are overestimated by inadequate airflow through a solar radiation shield. Thus when comparing two radiation shields, the shield with a better response time like the helical MeteoShield Professional, will produce higher maximums and lower minimums than all other naturally ventilated multi-plate solar shields without taking into account other affects. Fan-aspirated shields will have shorter response times in low wind conditions but are prone to evaporation errors from sucking in humidity with their forced ventilation.
Why does air temperature accuracy matter?
Conclusions arising from this analysis show that when temperature errors on sunny days reach 3°C in strong sun and low wind conditions such as found on sunny summer or winter days [1,2], these air temperature errors translate up to 16% errors in the amount of heat energy present in air. These errors are one of the reasons why thunderstorm formation, hail, tornadoes and hurricanes and their paths are hard to predict using today’s forecast models whose inputs are confounded by such large air temperature input errors.
To what degree is air temperature accuracy important?
Page 64 of the WMO CIMO-Guide No. 8 (2014 edition, Updated in 2017) contains WMO recommended response time and time constant of thermometers for atmospheric air temperature measurements as follows:
Section 2.1.3.3
Response times of thermometers For routine meteorological observations there is no advantage in using thermometers with a very small time-constant or lag coefficient, since the temperature of the air continually fluctuates up to one or two degrees within a few seconds (0.5 °C errors result if air temperature changes 2 °C over 30 seconds with a 20 second thermometer time constant). Thus, obtaining a representative reading with such a thermometer would require taking the mean of a number of readings, whereas a thermometer with a larger time-constant tends to smooth out the rapid fluctuations. Too long a time constant, however, may result in errors when long-period (short-period is more correct based on mathematics and experimets) changes of temperature occur. It is recommended that the time constant for thermometers, defined as the time required by the thermometer to register 63.2% of a step change in air temperature, should be 20 seconds. The time constant depends on the airflow over the sensor.
NOTE: It is not enough to have a time constant of 20 seconds at a hefty 3 m/s wind speed like the widely used HMP155 sensors. It needs to be at 1 m/s or less. It may be tolerable in a helical radiation shield or a fan-aspirated radiation shield, but not in any other atmospheric temperature measurement systems where air flow is usually much slower.
References
[1] Snow Albedo Effect on Air Temperature Measurements, Task 3.5 of the JRP ENV58 MeteoMet2 Project by C. Hofstättera, Chiara Musacchio, Andrea Merlone, Laura Massano, Graziano Coppac, Petra Milota of Bundesamt für Eich- und Vermessungswesen - Physico-technical Testing Service (PTP), Società Meteorologica Italiana, Istituto Nazionale di Ricerca Metrologica and Università degli Studi di Torino